学习《加密与解密》中密码部分遗留的问题
@TOC
前言
最近在看加密与解密的密码章节的时候,暴露出了自己以前遗留的密码学问题,再加上平常ctf中,涉及密码部分的题很多,就下定决心好好的把自己不会的恶补一下。于是,我就硬着头皮好好的去学习,学完发现,自己头皮还真硬
遗留问题

crc32
定义
数据通信领域中最常用的一种差错校验码
原理

例子

疑问
上面这些就是crc算法的原理,还是很好理解的,下面的内容才是我头皮硬的内容
通过学习 我又出现了以下的疑问
1什么是查表法 如何实现
2 crc的几个组成部分(多项式公式、多项式简记式、数据宽度、初始值、结果异或值、输入值反转、输出值反转、参数模型)怎么参与运算
解决
第一个问题:
在了解查表法之前,先学会直接计算法是如何在代码中实现的
这其中的核心原理就是利用了xor的交换律,使数据处理起来更加方便
1 | Const PLAY = &H1021& '这里生成项(实际上就是CRC-CCITT),注意这里默认首位1是去掉的 |
这下来看驱动表是如何得出的以及原理是什么
其实还是xor的交换律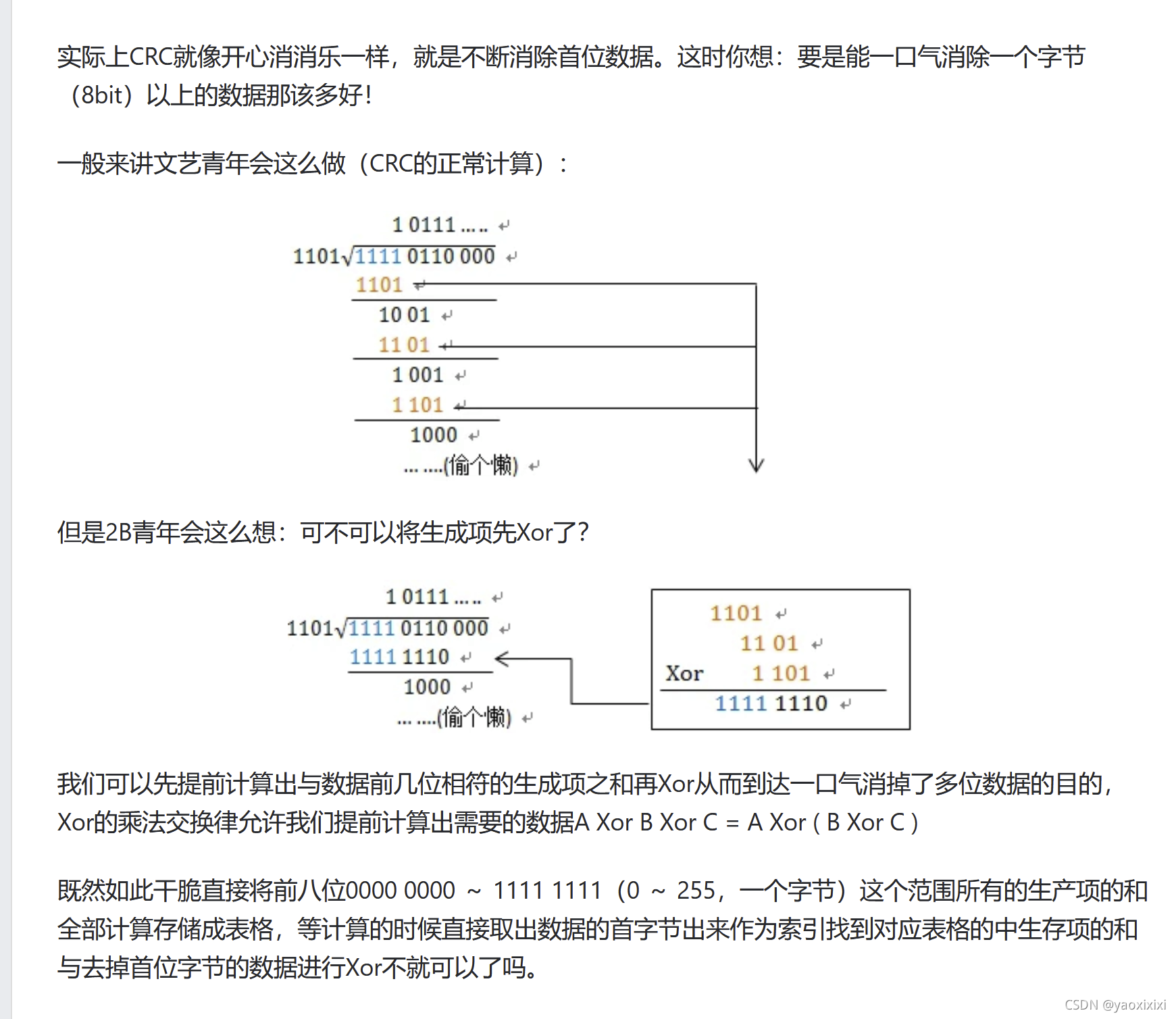

看了这么多,脑子都大了,本质来说,就是除数是固定的,直接计算后得出一个crc的校验码,这个校验码就是由除数的多重位移的异或和被除数异或得出来的,前者是固定的,而被除数是不固定的,所以前者是可以得出来的,那么把他存到一个表里,就可以省去很多计算步骤,类似动态规划的数组
那么我们只需要算以下步骤
第二个问题:
直接找到一篇文章学习
参考链接
https://www.cnblogs.com/masonzhang/p/10261855.html
https://segmentfault.com/a/1190000018094567
https://www.jianshu.com/p/2551ea7dbb14
总结
crc算法在实际运用中常见,但在re题目中不是特别经常能见到,不过2021的wmctf的re1就用了crc32,我们不需了解算法的全部细节,但是对于这种类型加密算法的敏感度应该提高
=.=(好吧,我明天就忘了
np问题
什么是p问题
什么是np问题
什么是npc问题
什么是p问题
可以在多项式的时间内解决的问题就是p问题
意思就是说如果数据翻倍的话,因为时间复杂度在多项式内,还是很快,不会因为数据爆炸,而导致速度急剧下降
什么是np问题
可以在多项式的时间内判断正确与否的问题
这里好比rsa的大数分解:
大数分解不好分,但是告诉你答案,这个大数可以分解为a和b ,那么你只需要一下就能判断a和b的乘机是否等于大数,这就是np问题
什么是npc问题
别人给出的解释
1 npc问题首先是个np问题
2 所有的np问题都可以约化为npc问题
我的理解是
1 npc问题可以说成np问题的集合,也是最难的的np问题的代表,意味着解决npc问题就可以解决np问题
2 npc问题是np问题和np-hard问题的集合
意思就是说np问题无法在多项式的时间内解决,这里再举个例子
要求遍历图中的每个点,并且返回起始点,求图中路线的最短距离
这里和上面那个rsa的不同之处在于,即使别人告诉了一条最短路径,你也无法确定他就是最短路径,只有当你把所有的最短路径列出来,才能知道答案
总结
np问题常用于公钥密码体制,我就简单的了解一下,发现计算机和数学还是密不可分啊
aes的加法和乘法是如何实现的
这个是之前学习aes遗留的小问题,其实反映的是我对于信息安全数学基础的那块知识没有理解透(光应付考试了,我透,现在后悔了
在aes的列混合操作里涉及到了矩阵的加法和乘法,他们不是我们平常意义上理解的加法和乘法,那是什么呢?(我也不知道
加法:就是两个数的异或
乘法: 通俗点来讲就是把其中一个数拆开 拆乘n多个字节的乘积,每个字节相加为原数(我猜的)
通俗点来讲就是把其中一个数拆开 拆乘n多个字节的乘积,每个字节相加为原数(我猜的)
好比:00000100=0000001000000010
00000011=0000001000000001
那么我们就可以转换为一个数和一个字节只有其中一位为1其他位为0(2的n次)的乘法
最后都化简到00000010
就可以参照上面那个算法
如果最高位为1就进行异或运算,否则不运行
这里还有一个问题就是 前者是如何得到后者的呢
前者是如何得到后者的呢
AES使用的有限域GF(2^8)是由GF(2)上8次不可约多项式生成的,
x^8 + x^4 + x^3+x+1
00011011就是x^4 + x^3+x+1
如果a7=1就表示S1是7次多项式,乘以x就会出现8次项,等于a6…a1左移一位再加00011011(就是x^4 + x^3 +x+1),系数再模2,相当于二进制比特串异或运算。
(我大概懂了吧……)
总结
有这么的问题其实是自己对域的本质运算不懂(现在也不懂)(学习中….
什么是群环域
群
一个集合,其中集合内的元素运算满足四条规律:封闭性,结合性,有单位元,逆元性
封闭性:不管怎么运算得到的数还是在集合中
结合性:可以更改运算顺序
有单位元:自己与单位元运算还是自己
逆元性:每个数都有逆元
环
一个环中涉及两个二元运算,分别是(R,+)与(R, ·)
前者是个交换群
后者是个半群
交换群=群+交换性
半群=封闭性+结合律
域
交换环,在乘法运算中加入了交换性
伽罗瓦域
有限元素的域
总结
什么是离散对数
欧拉函数

欧拉定理

什么是原根
https://baike.baidu.com/item/%E5%8E%9F%E6%A0%B9/8103534?fr=aladdin
和欧拉定理很神似。
离散对数
https://zhuanlan.zhihu.com/p/106967180


是不是和rsa贼像
一个离散对数的实例就是E1gamal 可以看书上的分析
什么是椭圆曲线和ecc算法
https://zhuanlan.zhihu.com/p/26029199
什么是椭圆曲线
椭圆曲线的方程
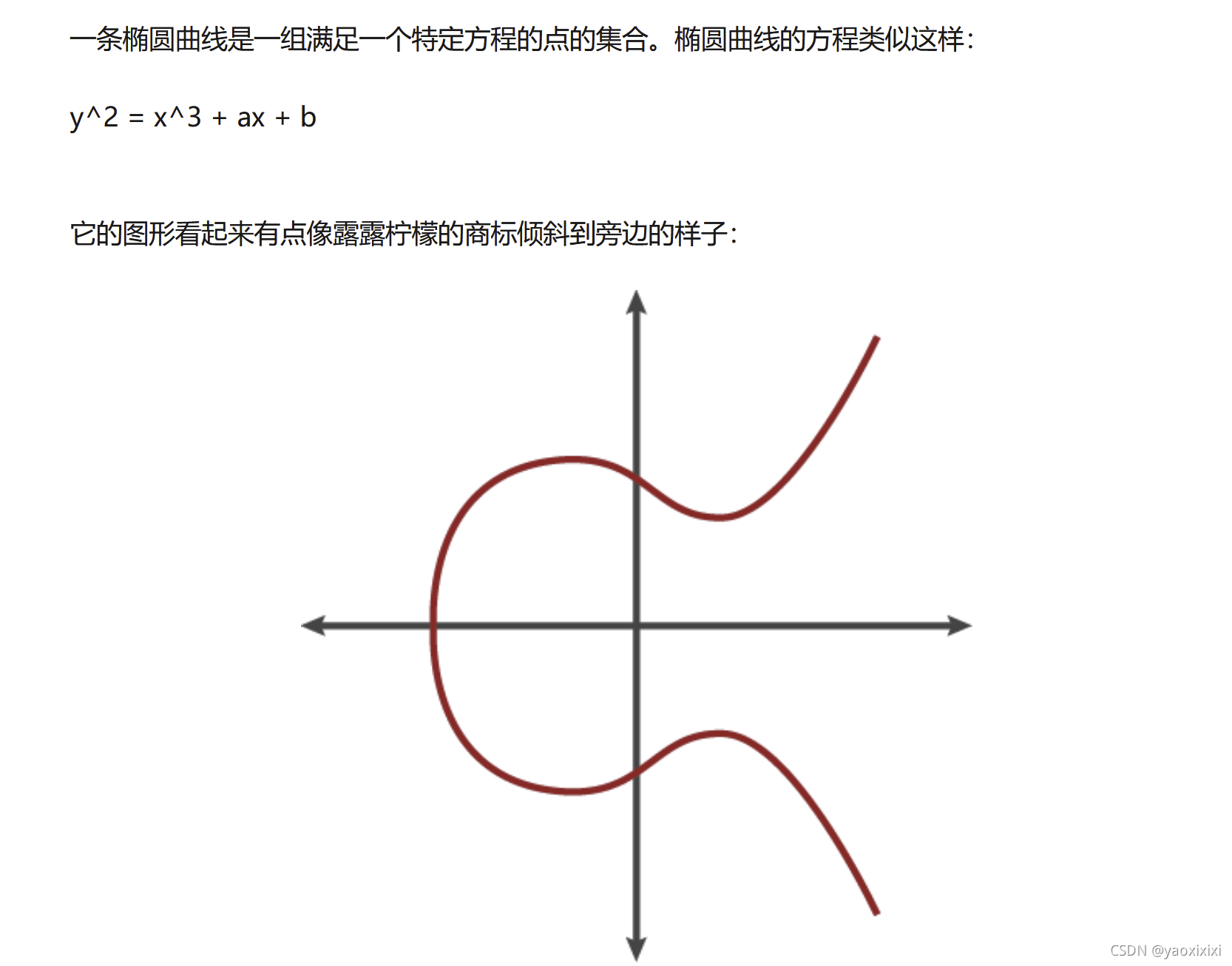
什么是ecc加密
首先我们需要3个参数
一个椭圆曲线方程,两个在椭圆曲线上的坐标 一个起点,一个终点,我们想要求打点次数
什么是打点 在文章中是这么描述的
在文章中是这么描述的
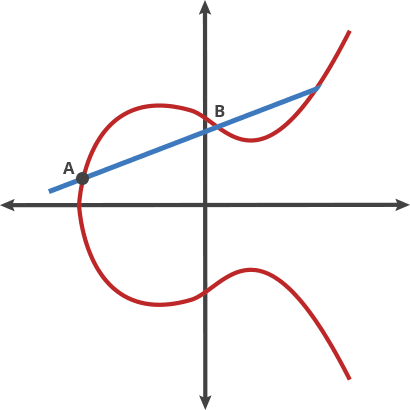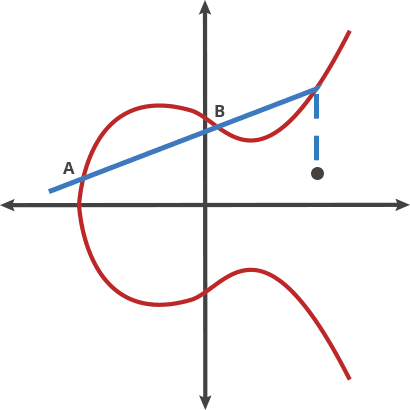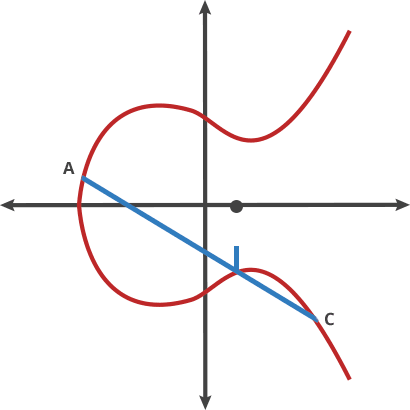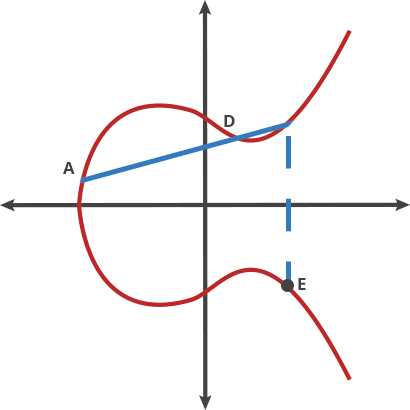
同样,正向是好推的,但是逆向确实十分困难的(具体的过程参考文章)
总结

最后
学习以上内容大概花费了我两天时间,其中有好多细节我还是没有学会,里面涉及的数学知识太多太多,再学就学偏了。由此可见,密码学真不是人学的……
我明显感觉到我又秃了,数学才是永远的神
